This article talked about how math is beginning to become more and more a bigger part of our everyday lives. One way it does this for example, is using math to analyze how well advertising is doing for a company, and how changing advertising can effect profits and sales. It is not limited to this though. Essentially what this article was saying is that math can be used to model and analyze just about everything in the world. Machines, productivity, security, sales, even humans. Another thing that I found really interesting was how important this math really is. The top mathematicians in the world, a select few, are becoming some of the highest paid people. I never would of thought that math would be getting you a 6 figure salary right out of college. This just goes to show how important and how helpful these models are for companies. Another thing it talked about is how these models can be an invasion of privacy, but I didn't really see how. For the most part, I see these models as looking at numbers not people. It turns people into numbers and so I don't really see the invasion of privacy, unless people feel invaded being turned into numbers. It is really interesting though, to think that everything can be justified with numbers.
This is one thing the article reminded me of was the movie Pi, an artistic, mind-blowing thriller about a paranoid mathematician who sees math everywhere and is one the verge of discovering the unifying number that explains everything. Here's a trailer:
The three points he makes about math being everywhere and thus it being able to explain the patterns everywhere in our world is pretty interesting, and relates back to this article. When I first saw this movie, I thought it was a little far-fetched, but now... I'm not so sure. The thing that really got me was that they're working on ways to model human behavior, a supposedly random and unpredictable thing. Maybe math is everywhere, maybe eventually we'll be able to see the patterns present in nature, and maybe someday we can use that knowledge of the patterns for the betterment of humanity and our world. We'll just have to wait and see.
Showing posts with label babar. Show all posts
Showing posts with label babar. Show all posts
Sunday, February 21, 2010
Monday, February 1, 2010
I Can See Clearly Now...
Welcome to my photos!
Just in case the titles and hot-spots aren't with the photos, I've put the link to Flickr underneath all my photos.

Here's the Link:
http://www.flickr.com/photos/47077084@N08/4310871956/

Here's the Link:
http://www.flickr.com/photos/47077084@N08/4310876542/

Here's the Link:
http://www.flickr.com/photos/47077084@N08/4310137659/

Here's the Link:
http://www.flickr.com/photos/47077084@N08/4310872732/

Here's the Link:
http://www.flickr.com/photos/47077084@N08/4320611099/
Just in case the titles and hot-spots aren't with the photos, I've put the link to Flickr underneath all my photos.

Here's the Link:
http://www.flickr.com/photos/47077084@N08/4310871956/

Here's the Link:
http://www.flickr.com/photos/47077084@N08/4310876542/

Here's the Link:
http://www.flickr.com/photos/47077084@N08/4310137659/

Here's the Link:
http://www.flickr.com/photos/47077084@N08/4310872732/

Here's the Link:
http://www.flickr.com/photos/47077084@N08/4320611099/
Sunday, January 31, 2010
Choices
1. For any point (a,b) on an invertible function, the derivative of the inverse of the function evaluated at b is equal to the reciprocal of the derivative of the function evaluated at a. In other words, the derivative of the inverse of a function is the reciprocal of the derivative of the function.
2. In symbols:

3. The function for volume of a sphere is below:

Yes, volume is an invertible function.
4.The inverse of this function:

5.

6. The slope of the tangent of the red function is 11.36, and I found the slope of the green function is .088, which is equal to 1/11.36.
7.I chose not to go to class. I've never done a virtual class before, so I wanted to see if I could effectively learn the class material without actually going to class. Also, by taking the virtual class I was able to sleep in, (this was really just a nice bonus). By utilizing my tools on the internet, I was able to learn the subject matter. The scribe post was also a very helpful tool. Overall, I think I was able to learn just as well in the virtual class, but had this been a more complicated, difficult topic, it's definitely helpful to have a teacher who knows what they are talking about.
2. In symbols:

3. The function for volume of a sphere is below:

Yes, volume is an invertible function.
4.The inverse of this function:

5.

6. The slope of the tangent of the red function is 11.36, and I found the slope of the green function is .088, which is equal to 1/11.36.
7.I chose not to go to class. I've never done a virtual class before, so I wanted to see if I could effectively learn the class material without actually going to class. Also, by taking the virtual class I was able to sleep in, (this was really just a nice bonus). By utilizing my tools on the internet, I was able to learn the subject matter. The scribe post was also a very helpful tool. Overall, I think I was able to learn just as well in the virtual class, but had this been a more complicated, difficult topic, it's definitely helpful to have a teacher who knows what they are talking about.
Friday, January 22, 2010
Forum Post: Cusp
Mark Twain once said, “Never let formal education get in the way of your learning.” While this statement is open to interpretation, I believe that when he refers to formal education he is referring to the standardized, static, and conformist education that we receive in schools. To a certain extent formal education has a set way to do things, there is no exploring, and there is no discovery. When he says that this ‘formal’ education gets in the way of learning, he is really saying that formal education gets in the way of discovery. True learning happens through experience, it happens through trial and error. It happens by trying new things, by taking risks, and by not holding yourself back. While formal education has its value, a teacher can only teach so much. At some point, we can only learn informally, but through our own passion. So what is the role of technology in all of this? Indeed, I think it has very much blurred the boundary between formal and informal learning. Using the Internet to learn is a form of informal learning, and while there can be a lot of very informal things on the Internet, one could also find many sites that are ‘formal’ education. Encyclopedias, databases, Calculus web-blogs, all these varieties of formal education can accessed informally through the Internet. Mark Twain may have felt that formal education is a limit on what we can learn. But in today’s world, where formal and informal education aren’t as easily differentiated, we can learn more than ever before, the sky is the limit.
Thursday, January 14, 2010
Quotient Rule Scribe Post
Have no fear… Scribe Post #2 is here! Today’s lesson was about The Quotient Rule.

In our exploration, we used the Product Rule in order to derive this rule that tells the derivative of a quotient of two functions. So before we go into that we should do a quick review of the Product Rule.

(Photo Credit: http://www.karlscalculus.org/qrule_still.gif)
Fig 1. (Awesome Picture)
Fig 1. (Awesome Picture)
In our exploration, we used the Product Rule in order to derive this rule that tells the derivative of a quotient of two functions. So before we go into that we should do a quick review of the Product Rule.
In Words: Take the derivative of the first function times the second plus the first function times the derivative of the second.
Short Form: y’=u’v+uv’
Ok, so now that we’ve got the product rule fresh in our minds let’s use it to find the derivative of a quotient property.
And so finally I present you with…
The Quotient Rule!!!
In Words:
The derivative of the numerator times the denominator minus the derivative of the denominator times the numerator, all divided by the denominator squared.
And just for fun, but also for education, here is a video I found that is a catchy tune for remembering this rule.
Well that’s all for today’s lesson. I hope it was helpful and informative. Leave comments and questions!
The next scribe is BlueElephants.
Tuesday, January 12, 2010
Product Rule
I Google searched the product rule and I clicked on the second search result, (the first was Wikipedia). It was a fairly dull looking website, but it was simple and to the point. First it stated the definition of the product rule, and was then followed by about 15 problems to work on. Each problem also had a link to a detailed solution, so I could easily check my work, or have something to go to if I got confused.
Here's the link to the site that I found:
http://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/productruledirectory/ProductRule.html
I think in this case the online source was more valuable to me, because it gave me the exact information I needed as well as an opportunity to try out that knowledge. The book does the same thing, but it also has a lot more information to navigate around.
One other thing I think is helpful, is being able to verbally define the Product Rule. This was not included in either the website or the book, but it can be done without them.
Here is Definition of the Product Rule:
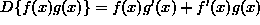
Example:
Differentiate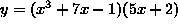 .
.
Solution:
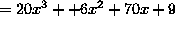
Here's the link to the site that I found:
http://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/productruledirectory/ProductRule.html
I think in this case the online source was more valuable to me, because it gave me the exact information I needed as well as an opportunity to try out that knowledge. The book does the same thing, but it also has a lot more information to navigate around.
One other thing I think is helpful, is being able to verbally define the Product Rule. This was not included in either the website or the book, but it can be done without them.
Here is Definition of the Product Rule:
Example:
Differentiate
Solution:
![]()
![]()
![]()
Subscribe to:
Posts (Atom)











