Personally, I found the website to be much better source for learning the product rule quickly and efficiently without compromising understanding. The book had much more lengthy and complete explanation of the product rule including graphs, verbal definitions, and symbolic definitions. Despite the thoroughness of the text book definition I still found the explanation on the website (http://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/productruledirectory/ProductRule.html) to be much more useful for a person like myself. The online resource gave one short definition, but many full length examples of increasing complexity. I found this to be more useful than the textbook for mainly that very reason. It is often easier for me to understand a new concept by looking at multiple examples that I can easily refer to if I find myself stuck on a problem. Another additional reason as to why I prefer the online resource is because it is simpler and makes the product rule in calculus look less daunting while maintaining the information necessary. Hence, the online resource, oddly enough, gives me somewhat more confidence in my understanding of the concept.
Product Rule:
The product rule is a formal rule for differentiating problems where one function is multiplied by another. The rule follows from the limit definition of derivative and is given by
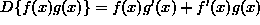
where D stand for the derivative of a function (excerpted from http://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/productruledirectory/ProductRule.html)
Example: Differentiate
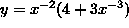
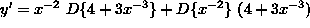
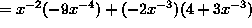
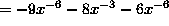
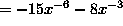
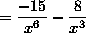
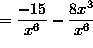
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Hey Casper,
ReplyDeleteI am impressed with the thoroughness of this post. You did an excellent job of explaining why the website was better for you and successfully articulated how that method integrated with your learning style(enough so that I am tempted to shift my own opinion seeing how I am of similar learning style). Excellent use of equation editor and your complex example demonstrates that you clearly understand the product rule. Also, good job remembering to cite your sources. Keep up the good work!
Hi mc Casper, the UC Davis website you referenced looks like an excellent resource! I like that you provide one of the examples, too. How did you choose that one to show? Is there something about the example that will make it easier for you to remember the Product Rule? What if you distributed the x^(-2) before taking the derivative? Does it yield the same answer? Could you use the Product Rule if you went that route? How?
ReplyDeleteThanks for the comment Cary!
ReplyDeleteI choose this example because it was one of the first few listed and was therefore a little simpler because the examples were in order of difficulty from easiest to hardest. I'm glad that you caught that you could first distribute the x^(-2). Most people think that in mathematics everything is black and white, but it often isn't! There are almost always multiple ways of analyzing and evaluating a problem which could all lead to the "correct answer" -I quite dislike the term correct answer because it is frustrating to me due to the fact that mathematics is about much, much more than getting that "correct answer"- we're tying to get. Either way, I tried out this different way of solving the problem and here is what I got.
x^(-2)(4+3x^(-3))
4x^(-2)+3x^(-5)
At this point you can no longer use the product rule because there are no functions multiplied together which are necessary in order to use the product rule. Instead, we can use the power rule to finish up the problem.
-8^(-3)-15x^(-6)
From here the the final few steps are the same as in the original example listed above.
Therefore, I must come to the conclusion that you can distribute the x^(-2) in order to get the same answer. But, if you do distribute x^(-2) you can no longer use the product rule to solve the problem.
Thanks again Cary!
mc Casper
p.s. I appologize for not using the equation editor in my comment. Does anybody know how to copy a downloaded image from sitmo into a comment? I couldn't figure it out. Maybe it's a mac thing (we have mac's as school computers here) because it won't even let me use my arrow keys to scroll through a comment I'm writting, which seems odd.